Skośność i kurtoza – jak interpretować rozkład danych

Rodzaje rozkładów danych

Rozkład normalny (krzywa Gaussa)

Rozkład normalny, często nazywany krzywą Gaussa, jest jednym z najczęściej występujących rozkładów w statystyce. W rozkładzie normalnym większość wyników jest skoncentrowana wokół wartości średniej, a liczba wyników maleje symetrycznie w miarę oddalania się od tej wartości. Średnia, mediana i moda w rozkładzie normalnym są równe.

Rozkład normalny jest często wykorzystywany w psychologii do analizy wyników testów psychologicznych, takich jak testy inteligencji czy testy osobowości, gdzie zakłada się, że większość ludzi uzyskuje wyniki bliskie średniej, a wyniki skrajne występują rzadziej.

Poniżej znajduje się przykład rozkładu normalnego, który jest jednym z najczęściej spotykanych w analizach statystycznych, zwłaszcza w psychologii, gdzie wiele zmiennych przyjmuje rozkład normalny.

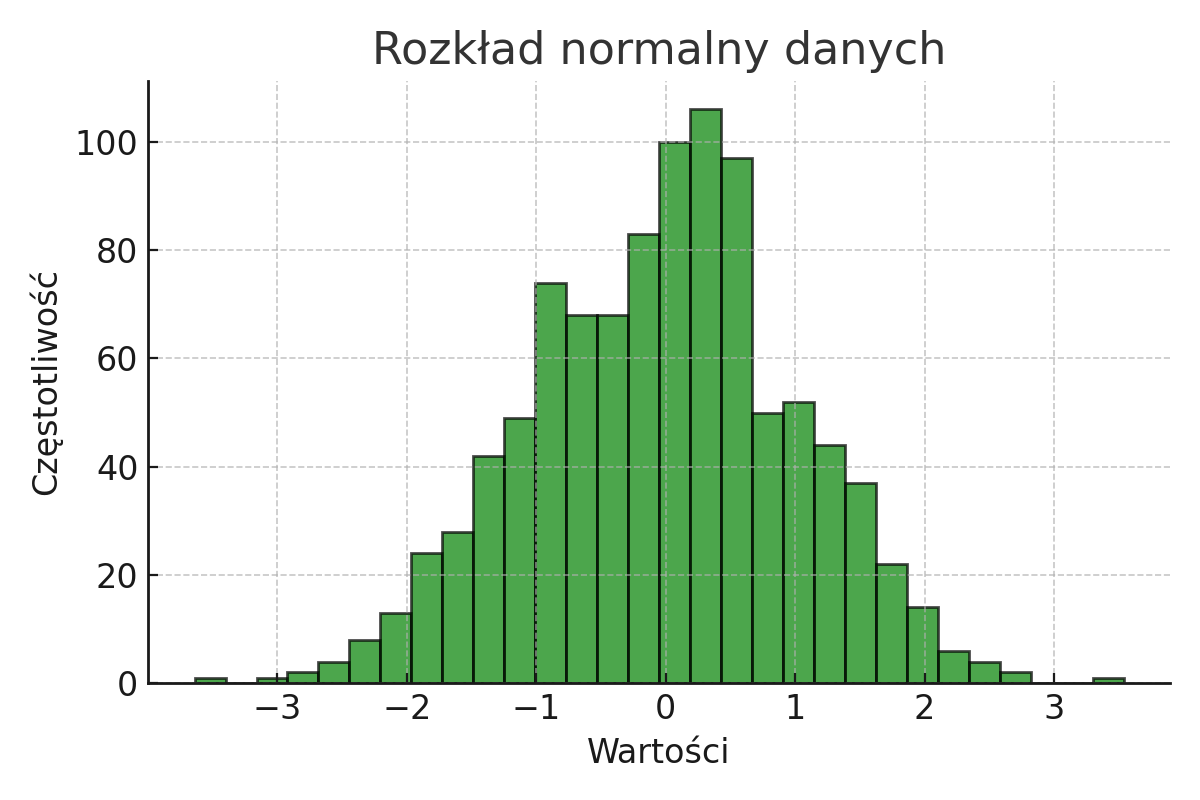
Przykład: W badaniach nad inteligencją rozkład wyników w populacji często przyjmuje kształt krzywej Gaussa, gdzie większość osób osiąga wyniki bliskie średniej, a jednostki o bardzo wysokim lub bardzo niskim ilorazie inteligencji występują rzadko.

Rozkład skośny (asymetryczny)

Skośność (ang. skewness) mierzy asymetrię rozkładu danych wokół średniej. Wskazuje, czy dane są bardziej rozłożone po jednej stronie średniej. Skośność obliczamy zgodnie ze wzorem:

S = ∑_i=1ⁿ ( ^{x_i - ̄x} / s )³ * n / ((n-1)(n-2))

Gdzie:

• S – skośność,
• n – liczba obserwacji w próbie,
• x_i – wartość każdej obserwacji,
• ̄x – średnia arytmetyczna próby,
• s – odchylenie standardowe próby.

Rozkład skośny pojawia się, gdy dane nie są symetrycznie rozłożone wokół średniej. Może być skośny w prawo (pozytywnie skośny) lub w lewo (negatywnie skośny). W rozkładzie skośnym wartości średniej, mediany i mody są różne, a większość wyników znajduje się po jednej stronie skali.

Poniżej znajduje się przykład asymetrycznego rozkładu danych, który często występuje w badaniach psychologicznych, np. przy analizie poziomów stresu czy lęku.

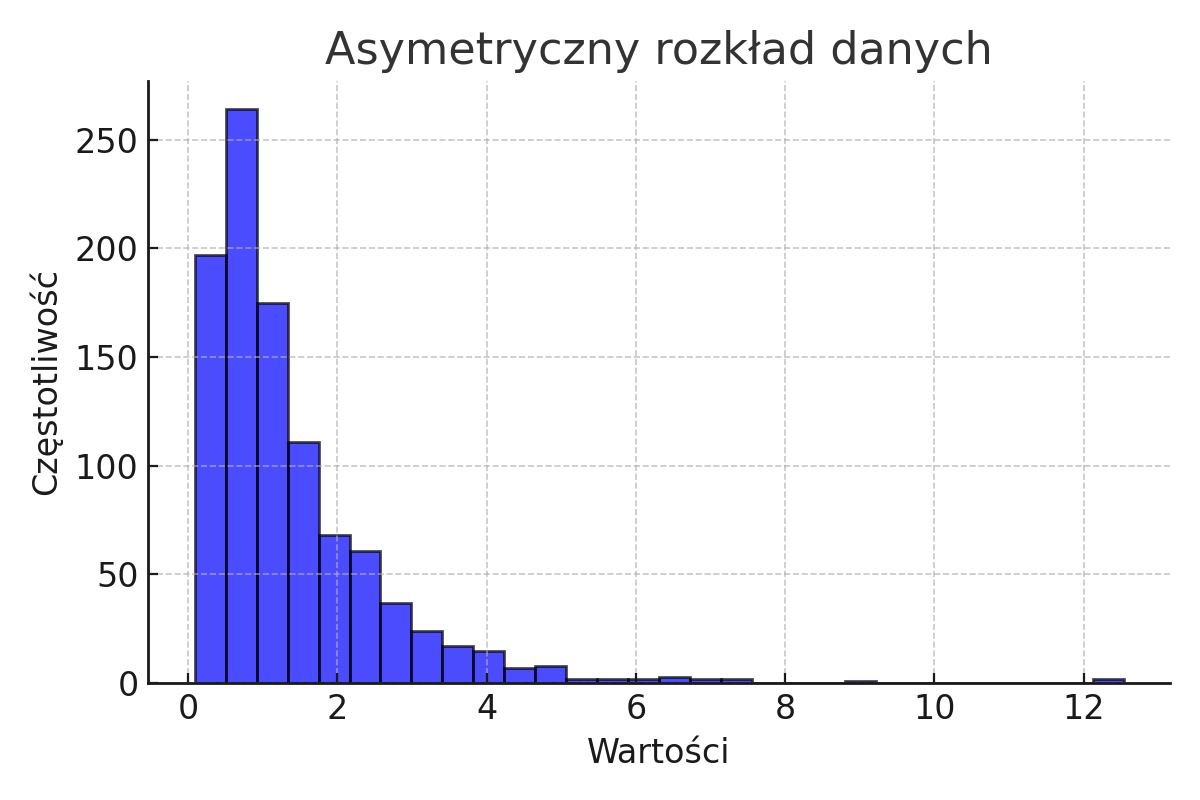
W psychologii rozkłady skośne są często spotykane, zwłaszcza w badaniach, w których mierzona zmienna ma naturalne ograniczenia, np. poziom stresu, który zazwyczaj nie może być ujemny i często jest bardziej skoncentrowany w niższych wartościach.

Przykład: W badaniach nad lękiem przed egzaminami u studentów większość wyników może skupiać się w dolnej części skali (niski poziom lęku), podczas gdy mniejsza część studentów doświadcza wysokiego poziomu lęku, co skutkuje pozytywną skośnością rozkładu.

Rozkład dwumodalny

Rozkład dwumodalny występuje, gdy w zbiorze danych znajdują się dwa różne, dominujące poziomy wyników, czyli ma dwa lokalne maksima. Może to oznaczać, że w populacji występują dwie różne grupy o odmiennych cechach.

W psychologii rozkład dwumodalny może wskazywać na istnienie dwóch różnych podgrup w badanej próbie, np. w badaniach nad satysfakcją z życia, gdzie jedna grupa może osiągać wysokie wyniki (bardzo zadowoleni) a inna niskie (niezadowoleni), co tworzy dwa wyraźne skupienia wyników.

Poniżej znajduje się przykład rozkładu dwumodalnego, który występuje, gdy w danych pojawiają się dwie dominujące grupy wyników. Jest to częsty rozkład w badaniach, które obejmują różne podgrupy populacji.

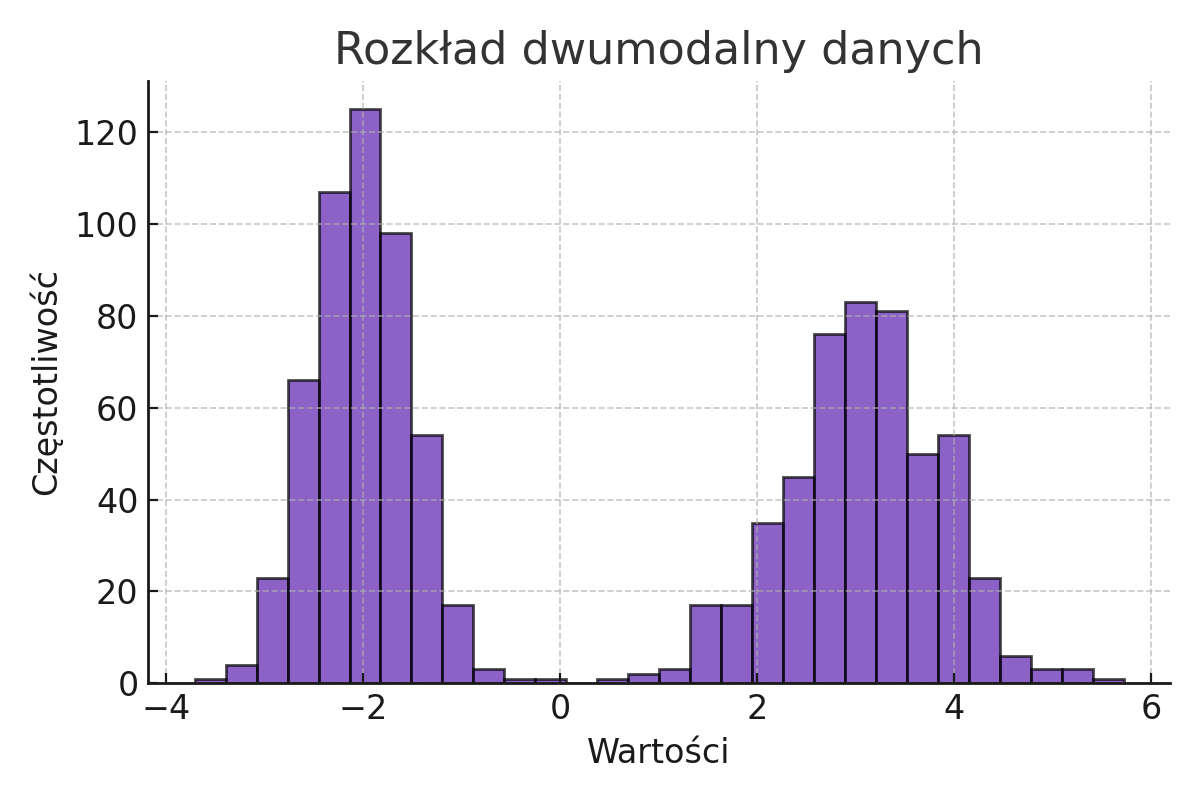
Przykład: W badaniach nad preferencjami stylów uczenia się uczniów, rozkład może być dwumodalny, jeśli badani preferują dwa różne style (np. wizualny lub kinestetyczny), co skutkuje dwoma dominującymi wynikami w populacji.

Rozkład leptokurtyczny i platykurtyczny

Kurtoza opisuje, jak "ostry" lub "płaski" jest rozkład danych w porównaniu do rozkładu normalnego. W rozkładzie leptokurtycznym dane są silnie skoncentrowane wokół średniej, co prowadzi do bardziej stromej krzywej. Z kolei rozkład platykurtyczny charakteryzuje się płaską krzywą, co oznacza, że dane są bardziej rozproszone. Obliczamy zgodnie ze wzorem:

K = ∑_i=1ⁿ ( ^{x_i - ̄x} / s )⁴ * n / ((n-1)(n-2)(n-3)) - 3

Gdzie:

• K – kurtoza,
• n – liczba obserwacji w próbie,
• x_i – wartość każdej obserwacji,
• ̄x – średnia arytmetyczna próby,
• s – odchylenie standardowe próby.

W psychologii leptokurtyczne rozkłady mogą wskazywać, że większość osób osiąga wyniki bliskie średniej, natomiast rozkłady platykurtyczne mogą sugerować większe różnice w badanej próbie.

Poniżej znajduje się przykład rozkładu leptokurtycznego, który charakteryzuje się dużym skupieniem wyników wokół średniej.

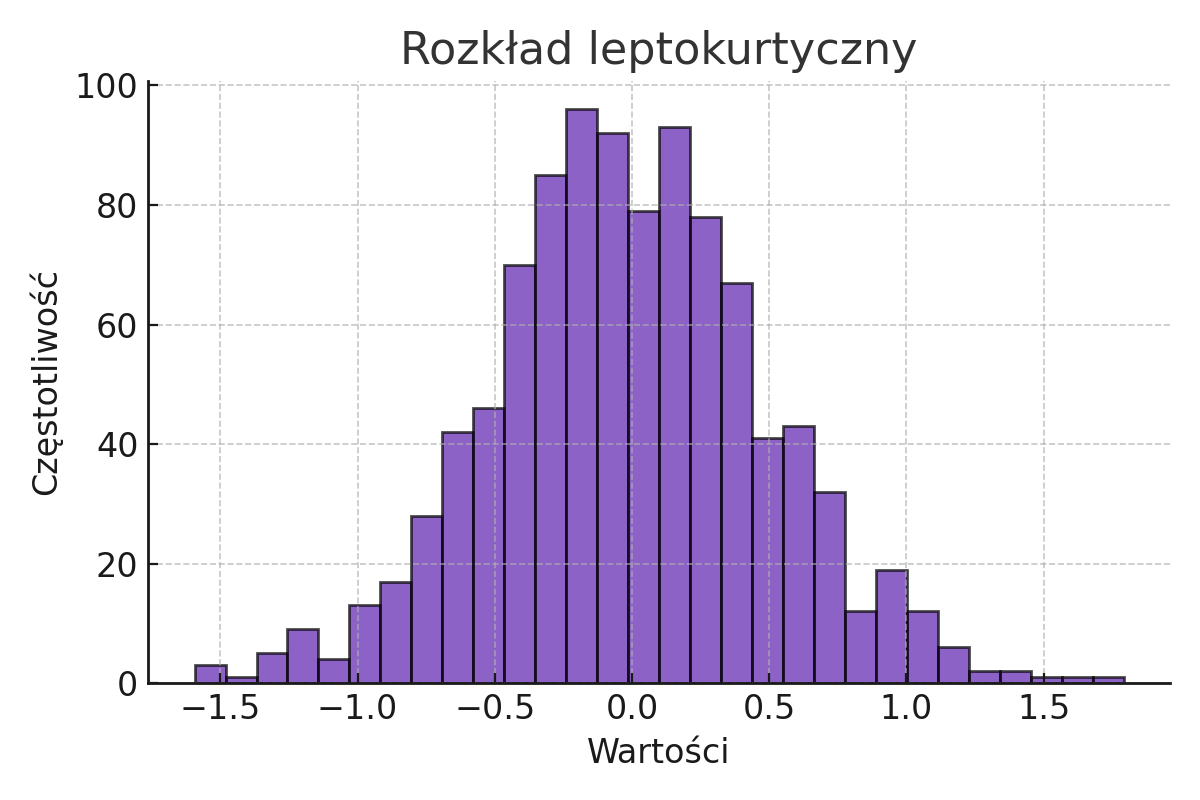
Poniżej znajduje się przykład rozkładu platykurtycznego, który wskazuje na większe rozproszenie wyników w porównaniu do rozkładu leptokurtycznego.

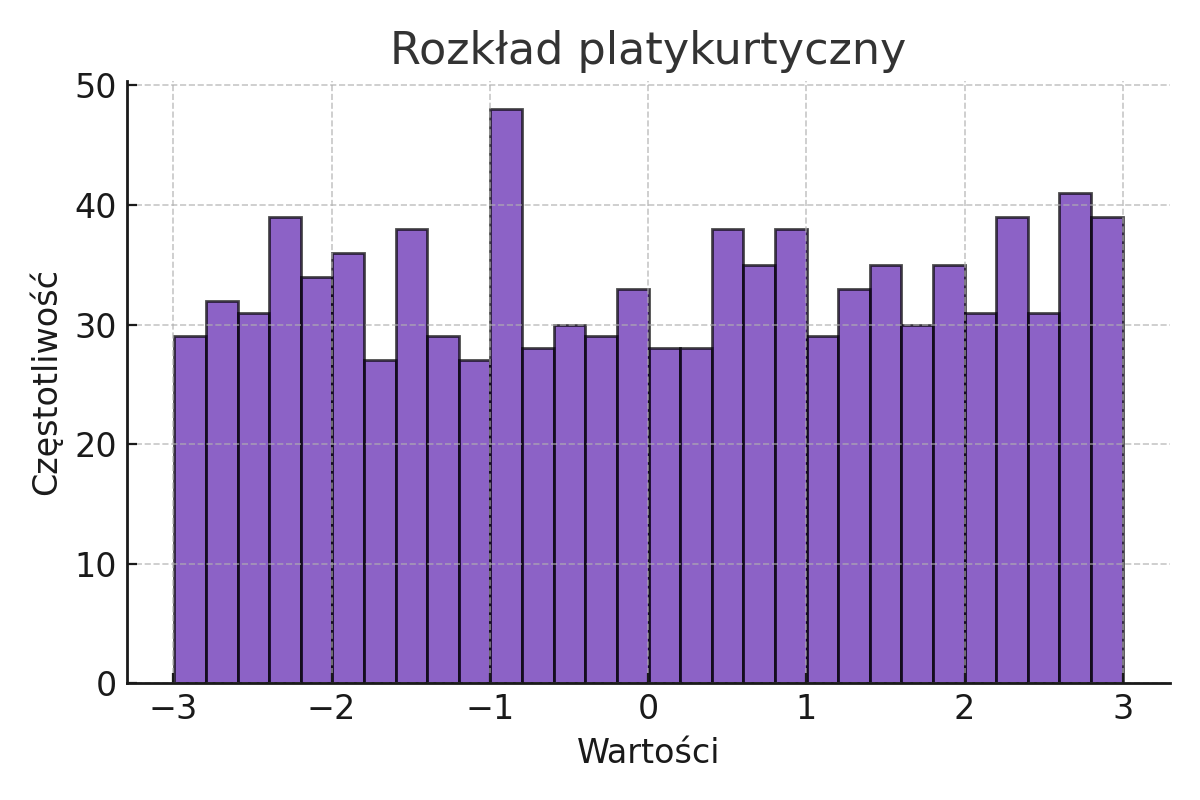
Przykład: W badaniach nad poziomem zadowolenia z pracy, jeśli większość pracowników ma podobny poziom zadowolenia, rozkład może być leptokurtyczny, natomiast jeśli zadowolenie jest zróżnicowane, rozkład będzie platykurtyczny.

Interaktywny rozkład wyników egzaminu

Zastosowanie rozkładów danych w analizie wyników

Zrozumienie rozkładów danych ma kluczowe znaczenie przy interpretacji wyników w pracach magisterskich i licencjackich. Wybór odpowiednich testów statystycznych zależy od rodzaju rozkładu danych, a znajomość rozkładów pozwala lepiej dopasować narzędzia analizy do charakterystyki badanej próby.

Na przykład, w badaniach empirycznych, które zakładają normalność rozkładu, możemy stosować testy parametryczne, takie jak test t-Studenta lub analiza wariancji (ANOVA). Natomiast gdy rozkład danych jest skośny lub nie jest symetryczny, zaleca się użycie testów nieparametrycznych, takich jak test Manna-Whitneya czy test Kruskala-Wallisa.