Homogeniczność wariancji – klucz do poprawnej analizy statystycznej

Czym jest homogeniczność wariancji?

Homogeniczność wariancji oznacza, że wariancje w różnych grupach badawczych są takie same lub zbliżone. W praktyce oznacza to, że zmienność wyników w różnych próbach, podgrupach lub kategoriach analizowanych zmiennych niezależnych nie różni się istotnie. Jest to kluczowe założenie wielu metod statystycznych, które zakładają równą zmienność w badanych populacjach.

Wykresy ilustrujące poziomy homogeniczności wariancji

Wysoka homogeniczność

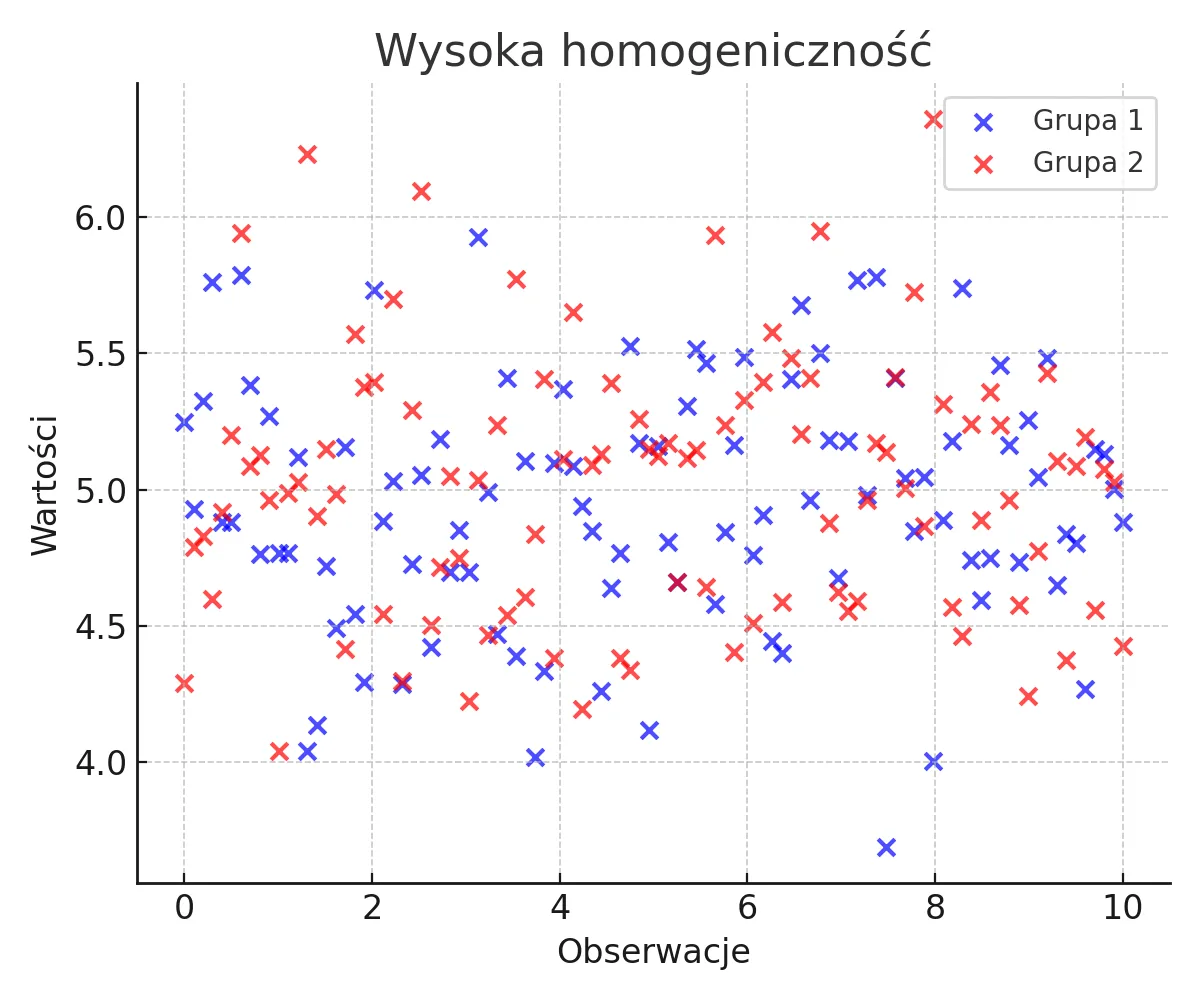
Grupy mają bardzo zbliżoną zmienność, co wskazuje na wysoką jednorodność wariancji.

Można zastosować testy parametryczne

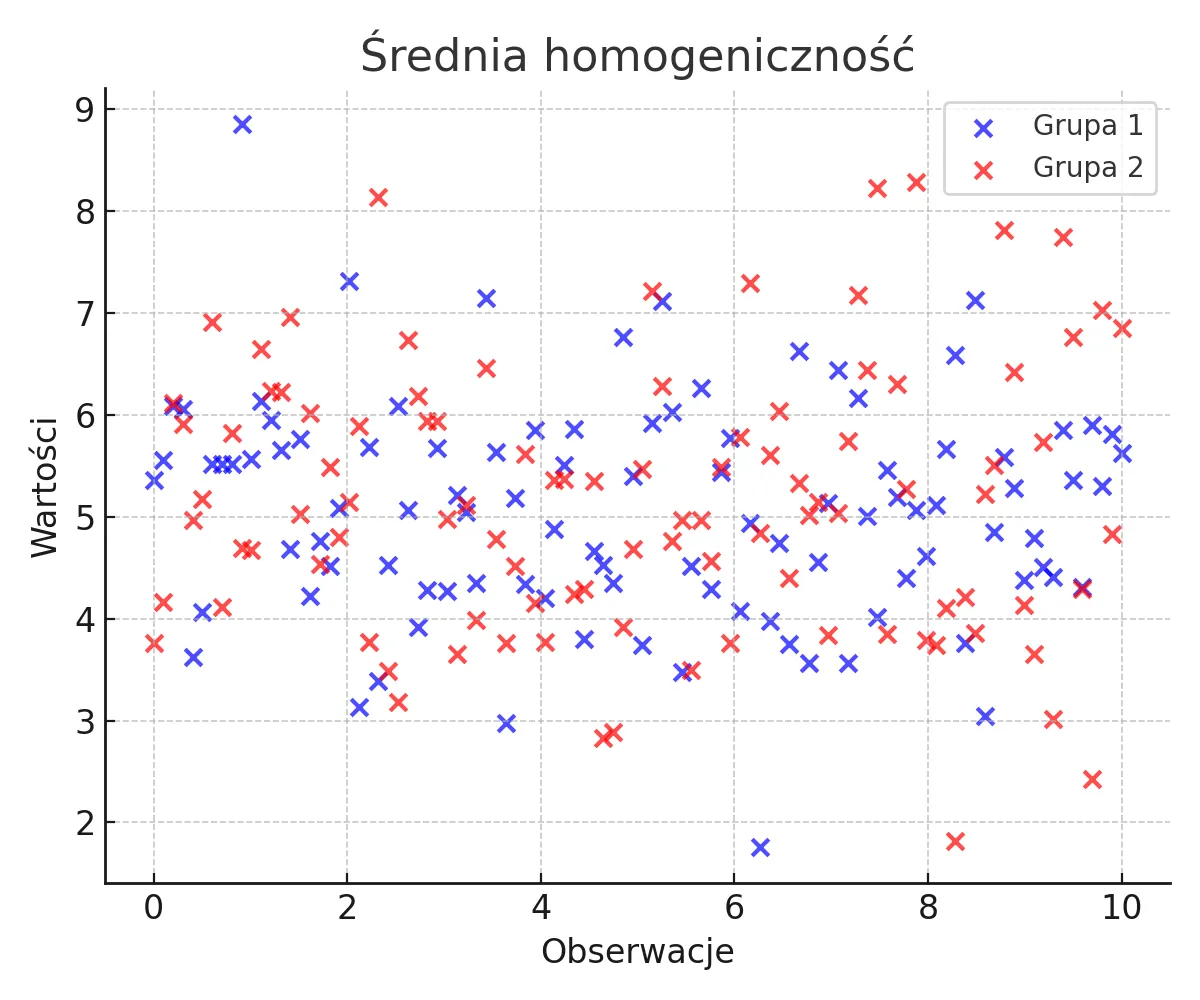
Średnia homogeniczność

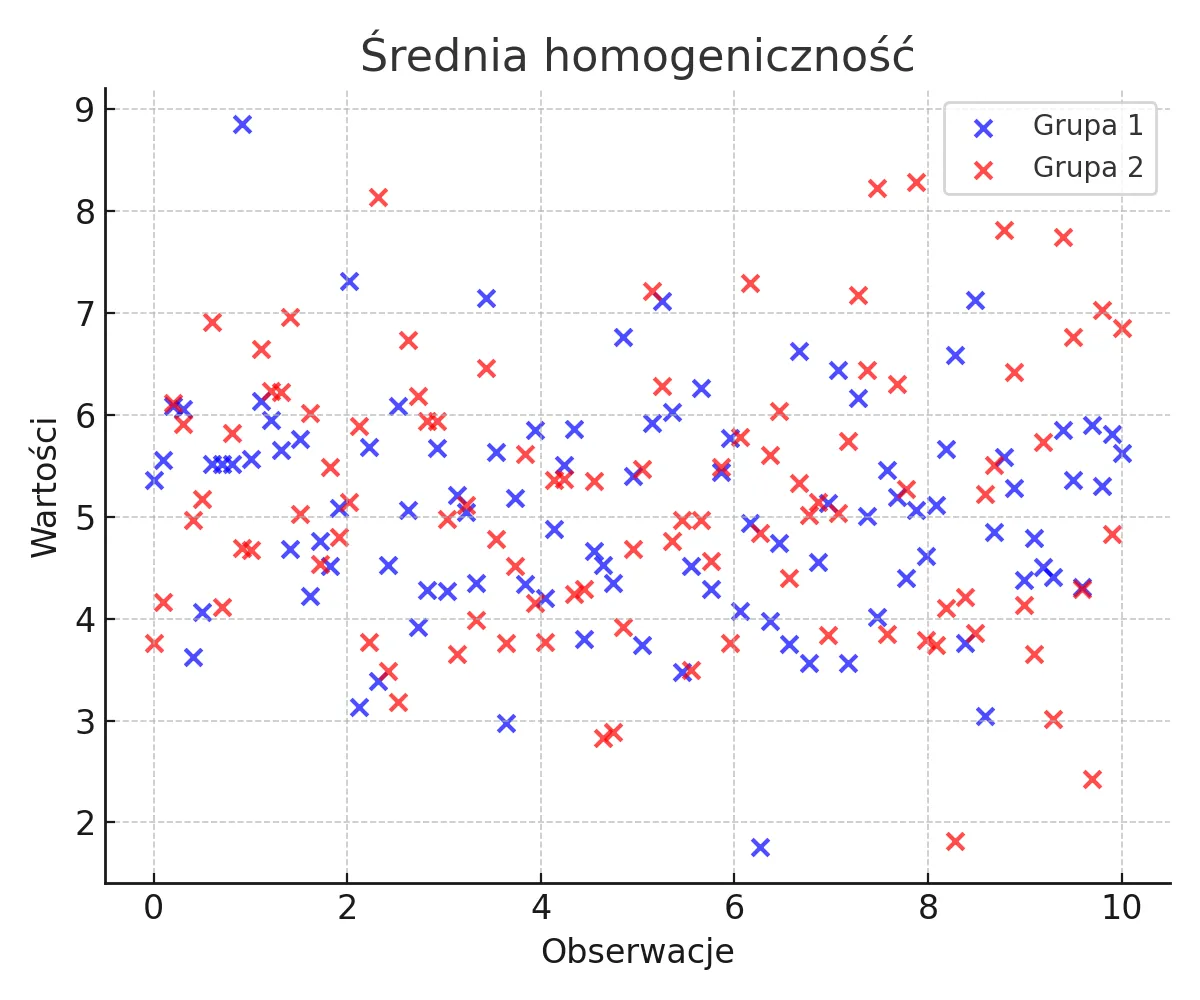
Grupy wykazują umiarkowane różnice w wariancji, co odzwierciedla średnią homogeniczność.

Nie można zastosować testów parametrycznych

Brak homogeniczności

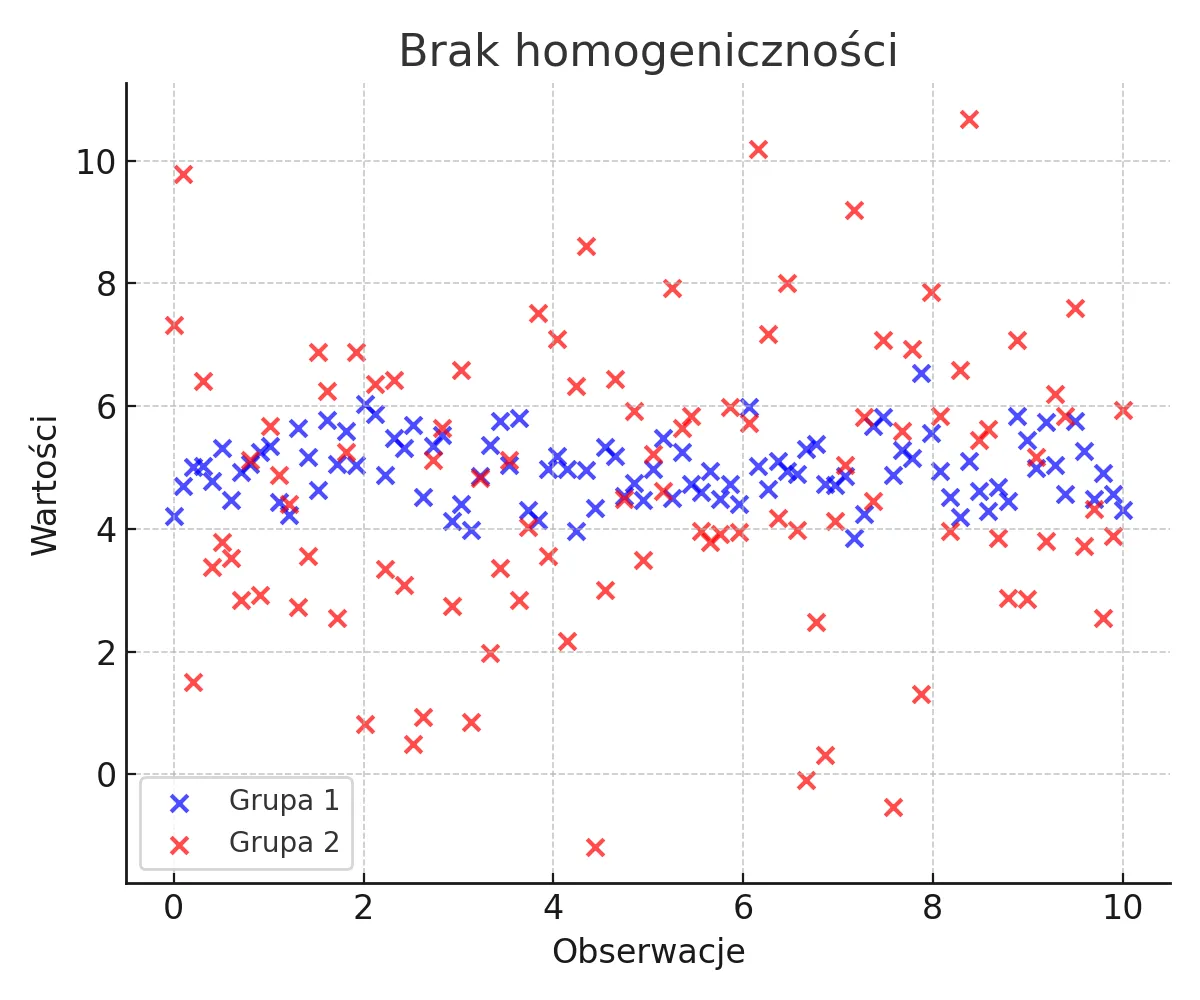
Grupy mają znaczne różnice w wariancji, co wskazuje na brak homogeniczności.

Nie można zastosować testów parametrycznych

Dlaczego jednorodność wariancji jest istotna?

Wiele testów statystycznych zakłada jednorodność wariancji, ponieważ naruszenie tego założenia może wpłynąć na:

• Wiarygodność wyników: Testy parametryczne stają się mniej odporne na błędy statystyczne, zwłaszcza gdy liczebność grup jest nierówna.
• Precyzję wnioskowania: Niejednorodność wariancji może prowadzić do zaniżania lub zawyżania wartości p, co wpływa na interpretację istotności statystycznej.
• Zwiększenie ryzyka błędu I rodzaju: Przyjęcie hipotezy alternatywnej, gdy jest ona w rzeczywistości fałszywa.

Testy statystyczne dla których wymagana jest analiza wariancji:

• Analiza wariancji (ANOVA)
• Test t-Studenta dla dwóch niezależnych prób
• Korelacja kanoniczna
• Modele liniowe (np. regresja wielokrotna)
• Testy jednorodności dla więcej niż dwóch grup
• MANOVA (wielowymiarowa analiza wariancji)
• Test F dla porównania wariancji

Testy weryfikujące homogeniczność wariancji

W analizie statystycznej stosuje się różne metody weryfikacji jednorodności wariancji, m.in.:

• Test Levene’a: Jest najczęściej stosowaną metodą weryfikacji homogeniczności wariancji. Porównuje odchylenia bezwzględne od mediany w każdej grupie, co sprawia, że jest odporny na odstępstwa od normalności.

  Przykładowe wyniki testu Levene’a:

  Zmienne zależne	Statystyka F testu Levene’a.	df międzygrupowe	df wewnątrzgrupowe	p
  Wynik testu	3.567	2	57	0.035
  Ocena końcowa	1.234	3	56	0.302

  Legenda: Statystyka F testu Levene’a - stosunek zmienności międzygrupowej do wewnątrzgrupowej, df międzygrupowe - stopnie swobody między grupami, df wewnątrzgrupowe - stopnie swobody wewnątrz grup, p - istotność statystyczna.

  Wynik testu Levene’a: Statystyka F wykazała brak jednorodności wariancji między grupami (F(2, 57) = 3.57, p = 0.035). Otrzymana wartość p jest mniejsza niż poziom istotności α = 0.05, co pozwala odrzucić hipotezę zerową o jednorodności wariancji. W konsekwencji należy rozważyć zastosowanie metod statystycznych odpornych na brak jednorodności, takich jak test t-Studenta z korektą Welcha lub testy nieparametryczne.

  Dla zmiennej Ocena końcowa wyniki wskazują na jednorodność wariancji (F(3, 56) = 1.23, p = 0.302), ponieważ wartość p przekracza poziom istotności α = 0.05. Oznacza to, że można stosować testy parametryczne przy analizie tej zmiennej.

• Test Bartletta: Jest bardziej czuły na naruszenia założenia normalności, co sprawia, że lepiej sprawdza się w sytuacjach, gdy dane mają rozkład normalny.
• Test F-Max Hartleya: Porównuje stosunek największej wariancji do najmniejszej w badanych grupach. Jego stosowanie zaleca się przy niewielkiej liczbie grup i równych liczebnościach prób.
• Test Brown-Forsythe’a: Jest modyfikacją testu Levene’a, bardziej odporną na odstępstwa od normalności.
• Grafy diagnostyczne: Analiza wykresów, takich jak wykresy pudełkowe, może być pomocnym narzędziem w ocenie wizualnej jednorodności wariancji.

Co zrobić w przypadku naruszenia homogeniczności wariancji?

Jeśli dane naruszają założenie homogeniczności wariancji, istnieje kilka możliwych podejść:

• Zastosowanie testów nieparametrycznych: Testy nieparametryczne, takie jak test Kruskala-Wallisa czy test Manna-Whitneya, nie wymagają spełnienia założenia jednorodności wariancji.
• Korekta w metodzie parametrycznej: W przypadku testu t-Studenta można zastosować korektę Welcha, która pozwala na analizę przy niejednorodnych wariancjach.
• Transformacja danych: Logarytmowanie, pierwiastkowanie lub inne transformacje mogą pomóc w redukcji różnic w wariancjach.
• Zastosowanie modeli mieszanych: Modele liniowe z efektami mieszanymi pozwalają uwzględnić różnice w wariancjach między grupami.

Podsumowanie

Homogeniczność wariancji to kluczowy element analizy statystycznej, którego naruszenie może wpłynąć na wiarygodność wyników badania. Przed przeprowadzeniem analizy należy zawsze zweryfikować to założenie za pomocą odpowiednich testów. W sytuacjach, gdy założenie jednorodności wariancji nie jest spełnione, warto sięgnąć po alternatywne metody analizy, które uwzględniają różnice w wariancjach.

Artykuł ten ma na celu uświadomienie badaczom znaczenia weryfikacji jednorodności wariancji oraz przedstawienie praktycznych narzędzi i rozwiązań na wypadek jej naruszenia.